

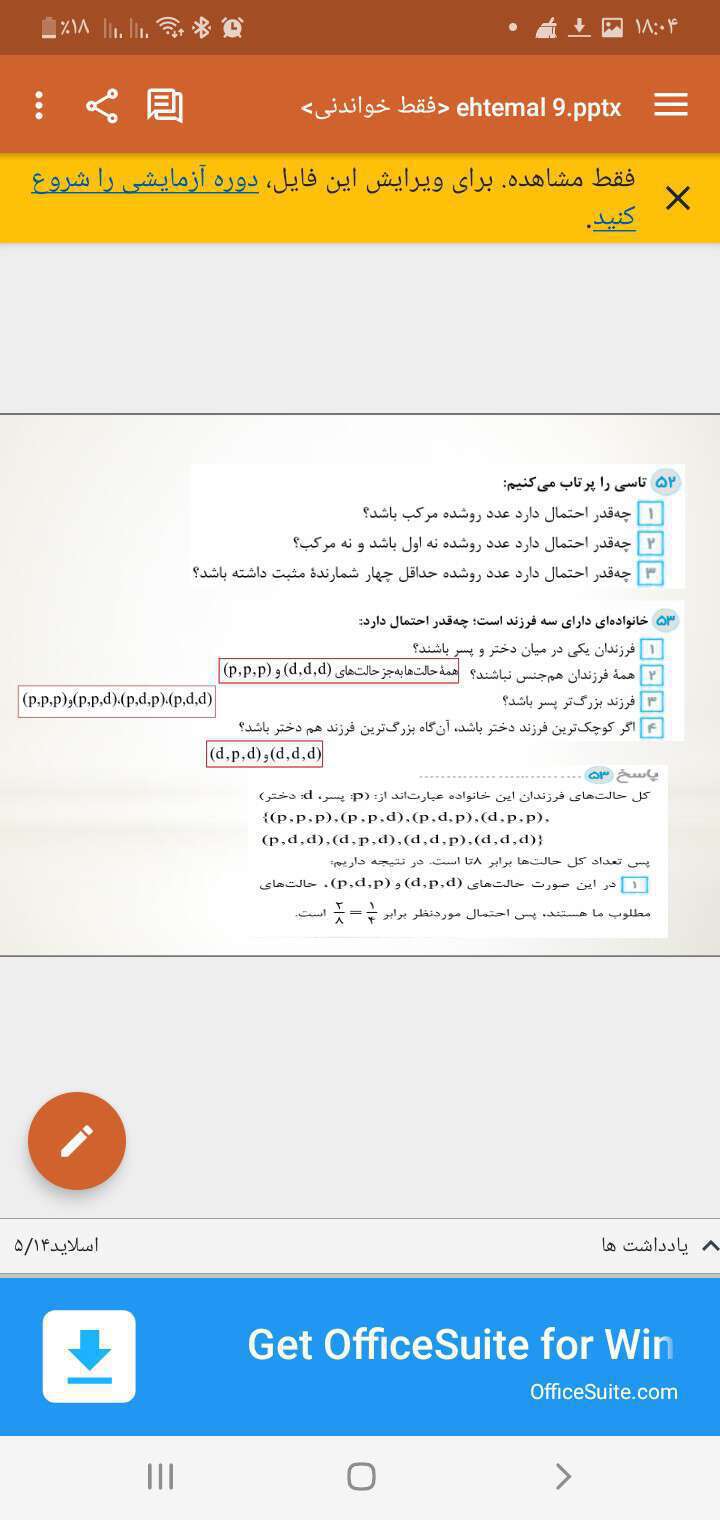

دو به توان سه میشه تعداد حالت هایی که سه فرزند خانواده رو نشون داد.یعنی
(د، د، د) (د، د، پ)(د، پ، پ) (پ، پ، پ) (پ، پ، د) (پ، د، د)
(د، پ، د) (پ، د، پ) که برابر با 8 حالته
در صورتی که زیر مجموعه یک مجموعه n عضوی(که اعضا متمایز هستند) هم از رابطه دو به توان n بدست میاد مثلا:
مجموعه:{1،2،3}
زیر مجموعه ها:
{1}{2}{3}{1،2}{2،3}{3،1}{1،2،3}{ } که تعدادشون برابر3^2=8 میشه. (زیر مجموعه اخر منظور همان تهی است)


برداشت شما و فرمولتون برای تعداد حالت هایی که میشه برای ترتیب فرزندان خانواده در نظر گرفت، درست بود ولی نمیشه بهش گفت تعداد زیرمجموعه ها، چون زیر مجموعه میتونه شامل تهی و یک یا دو عضو هم باشه درصورتی که برای n عدد فرزندان یک خانواده، باید همه n عدد رو استفاده کرد.
ولی این فرمولی که گفتین برای تعداد زیر مجموعه ها هم صادقه، یعنی فرمول "دو به توان n" هم برای تعداد 'حالت' های فرزندان خانواده و هم برای تعداد 'همه زیرمجموعه های' یک مجموعه درسته.
