پاسخ
باید پرسشها را طوری طرح کرد که در هر پرسش، انواع ممکن عددها نصف شود. در این صورت اگر 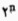 عدد ممکن باشد، n پرسش کافی است
عدد ممکن باشد، n پرسش کافی است
چون طبق شرط روی هم 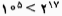 شماره مختلف تلفن وجود دارد، 17 پرسش کافی است. (دقت کنید که اگر 17 بار عدد 100000 را بر 2 تقسیم کنیم، حاصل عددی کوچکتر از 1 می شود).
پرسشها را با روشهای متفاوت می توان انجام داد، مثلا می توان پرسید: «آیا درست است که شماره تلفن شما از 50000 بزرگتر است؟» و اگر جواب داد «بله»، پرسش دوم را به این صورت که «آیا از 75000 بزرگتر است؟» و غیره.
شماره مختلف تلفن وجود دارد، 17 پرسش کافی است. (دقت کنید که اگر 17 بار عدد 100000 را بر 2 تقسیم کنیم، حاصل عددی کوچکتر از 1 می شود).
پرسشها را با روشهای متفاوت می توان انجام داد، مثلا می توان پرسید: «آیا درست است که شماره تلفن شما از 50000 بزرگتر است؟» و اگر جواب داد «بله»، پرسش دوم را به این صورت که «آیا از 75000 بزرگتر است؟» و غیره.
حالا ثابت می کنیم که 16 پرسش کافی نیست. در حقیقت ترکیبهای مختلف 16 کلمه «بله» و «نه» برابر است با 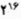 و چون
و چون  ، دو شماره مختلف تلفن، منجر به یک نوع جواب می شود و برای ما هیچ امکانی وجود ندارد که بدانیم کدامیک درست اند.
، دو شماره مختلف تلفن، منجر به یک نوع جواب می شود و برای ما هیچ امکانی وجود ندارد که بدانیم کدامیک درست اند.
روش «نصف کردن» که در اینجا از آن استفاده کردیم، برای بسیاری از مساله ها به کار می رود، مثلا وقتی که بخواهیم فرد مشخصی را در مقابل پاسخهای مثبت یا منفی یکی باشد. مثلا نباید از این پرسش شروع کرد که «آیا این شخص زیست شناس است؟» بلکه خیلی بهتر است که بپرسیم : «آِیا دانشمند است؟»
روش دیگر: ساده تر این است که از دستگاه عدد شماری به مبنای 2 استفاده کنیم، که در آن تنها از دو رقم 0 و 1 استفاده می شود. هر عدد کوچکتر از 100000 در این دستگاه، حداکثر با 17 رقم 0 یا 1 نوشته می شود. می توان پرسشها را این طور انجام داد:
1) آیا درست است که آخرین رقم شماره تلفن در دستگاه عدد شماری به مبنای 2 مساوی واحد است؟
2)آیا رقم ما قبل آخر شماره تلفن واحد است؟ و غیره.

 مریم اخوان طاهری
مریم اخوان طاهری
4 پرسش

سلام مریم عزیز
لطفا جوابی که برای معما ارسال می کنید را با دلیل بیان کنید و در صورت امکان تصویر راه حل تونو بفرستید تا بقیه دوستان هم در موردش نظر بدن.
ممنون
(راهنمایی: جواب شما درست نیست.)
 فرانک سلاحی
فرانک سلاحی
سلام
وقتتون بخیر
شاید کمترین پرسش ،1 پرسش باشد و 5 رقم شماره ،ارقام یکسانی باشه و فرد در اولین حدس اونو رقم رو بگه مثلن
شماره دارای 5 رقم 6 هست؟ و جواب بله باشه

سلام فرانک عزیز
لزوما اینطور نیست، بایستی پاسخی را در نظر بگیریم که در هر حالت به شماره دست پیدا کنیم.
ممنون از شما
 مهدیه آزرمجو
مهدیه آزرمجو
هر کسی میتونه چند جواب داشته باشه؟

سلام مهدیه عزیز
بله همینطوره، پیروز باشی
 بهار پورعلی
بهار پورعلی
خب بستگی داره
مثلا برای یکان می پرسیم که عدد مورد نظر زوجه یا فرد
اگه گفت زوج که ما پنج تا سوال باید بپرسیم یعنی پنج سوال 0/2/4/6/8
و اگه گفت فرد ما چهار تا سوال باید بپرسیم یعنی چهار سوال 1/3/5/7/9
و همین طور ادامه داره
این نظر من بود

سلام بهار عزیز
ممنون از شما، توضیحات تون بررسی شد و راه حل مورد نظر شما برای این معما کامل نیست.
لطفا جواب ارسالی مریم عزیز رو بخونید و نظرتونو بگین.
پیروز باشی
 مریم رضائی
مریم رضائی
۱۷سوال کمترین تعداد پرسشی هست که میشه با جواب بله و خیر انجام داد؛تا مطمئن شد میشه عدد رو با این ۱۷ سوال فهمید؛میدونیم شماره دوستمون ۵ رقمیه؛حالا اگه منظور عدد ۵ رقمی باشه که تعداد حالت های ممکن برای شماره دوستمون میشه 90000حالت و اگه شماره دوستمون به صورت کد باشه میشه 100000 حالت چون اولین رقم از سمت چپ میتونه صفر هم باشه؛در اینجا جواب برای هردو حالت ۱۷ سواله؛دلیلش اینه که ما برای این که مطمئن بشیم عدد رو میفهمیم باید سوالا طوری طراحی بشه که پس از آخرین سوال فقط یک حالت برای عددمون باقی مونده؛و اگر که ما بخوایم برای هر عدد یک حالت از جواب سوال هامون رو هم در نظر بگیریم؛باید تعداد حالت های جواب سوال هامون برابر با تعداد حالت های ممکن جواب باشه؛بنابراین تعداد حالت های جواب های سوال هامون باید حداقل به تعداد حالت های ممکن برای شماره ۵ رقمی باشه؛در این صورت میشه برای هر ۵ رقم یک حالت جواب در نظر گرفت و فهمید اون ۵ رقم چه ارقامی هستند؛خب از اونجا که نوع جواب های ما بله خیر و دو حالتی هستند؛ تعداد حالت های جوابمون براب با ۲ به توان تعداد پرسش هایی هست که میپرسیم؛ وبنابراین
دو به توان n باید بزرگتر مساوی90000باشه(اگه عدد ۵ رقمی باشه)
دو به توان n باید بزرگتر مساوی 100000باشه(اگه کد ۵ رقمی باشه)
و برای هردو حالت کوچک ترین nطبیعی ممکن ۱۷ هست؛بنابراین میشه با ۱۷ سوال فهمید اون پنج رقم کدوم ارقامن

سلام مریم عزیز
ممنون از توضیحات کامل شما، خیلی خوب و زیبا تفسیر کردید.
بچه هایی که با مریم موافقن، جواب ایشونو لایک کنن.
 علی یوسفی
علی یوسفی
سلام
برای هر عدد اینگونه باید سوال بپرسیم.
بالای پنج است یا نه
زوج است یا نه
پایین عددی که در جواب بالا به دست آورده ایم است یا نه
برای هر عدد 3 سوال که در کل 15 سوال میشه

سلام، دوستان تا حدی علی به جواب نزدیک شده، کسی نظری نداره؟
 عسل پوراسحاقی
عسل پوراسحاقی
با سلام و عرض ادب و احترام
وقتتون بخیر
15 پرسش مطرح شده
هر رقم را به طور جداگانه بدست می آوریم
و برای بدست اوردن هر رقم سه پرسش مطرح میکنیم
1_ رقم مورد نظر زوج است ؟
2 _ رقم مورد نظر بیشتر از 5 است ؟
3_ رقم مورد عدد اول است ؟
3 پرسش برای بدست اوردن هر رقم و چون 5 رقم بوده است مجموعا 15 پرسش مطرح شده
باتشکر

سلام
با این روش نمیشه عدد رو بدست آورد، مثلا اگر رقم یکان شماره دوستمون 6 باشد، با این 3 پرسشی که شما مطرح کردید می تونیم به اعداد 6 و 8 برسیم، بنابراین کافی نمی باشد.
 مریم رضائی
مریم رضائی
در جواب سوالی که درباره ی نظر آقای یوسفی پرسیدیدشب ۲ سوال اولی که ایشون پرسیدن به گونه ای هست بعد از جواب دادن ممکنه ۳ حالت برای رقم انتخابی پیش بیاد و در ایمن صورت سوال سومی که میپرسن هرچه که باشه نمیتونه رقم رو به صورت یکتا تعیین کنه؛چون در جواب دو حالت بله خیر وجود دارد و چون ۳ حالت ممکن است بهترین سوال را هم که بپرسیم یکی از جواب های بله یا خیر نشون دهنده ی دو حالت میشه و بنابراین جواب رو به صورت یکتا مشخص نمیکنه؛و بعد از این ۱۵ سوال ۳۲ حالت برای جواب ممکن است و حتی با پرسیدن دو سوال دیگه در کنار این ۱۵ سوال هم نمیشه عدد رو پیدا کرد چون بهترین سوال هارو هم که بپرسیم ۸ حالت برای جواب ممکن است وشماره به صورت یکتا تعیین نمیشه؛در اینجا با این که ۱۷ سوال هم پرسیده شد ولی جواب به طور یکتا پیدا نشد چون سوال ها به بهترین صورت پرسیده نشدند؛اگه سوال ها به بهترین صورت پرسیده بشن با ۱۷ سوال میشه عدد رو پیدا کرد بالاتر هم اثبات رو گفتم؛مثلا یکی از روش های بهینه که در ۱۷ سوال که کم ترین حالت هست میشه این جواب رو پیدا کرد اینه که این کار رو انجام بدیم:(اگه جواب به صورت کد باشه و رقم صفر هم بشه در پنجمین رقم از سمت راست قرار داد)
اول برای هر رقم بپرسیم آیا این رقم زوج است؟با پرسیدن این سوال برای هر رقم به طور جداگانه برای هر رقم ۵ حالت به وجود میاد و برای شماره 5به توان۵ حالت به وجود میاد؛برای پرسیدن سوال های ششم تا هفدهم به صورت زیر عمل می کنیم
دوازده تا مجموعه درست می کنیم به نام هایA6تاA17و در پرسش های ششم تا دوازدهم به این صورت سوال می پرسیم
در پرسش n ام می پرسیم آیا شماره شما عضو مجموعه ی An هست؟
وبرای تعیین اعضای مجموعه ها به این صورت عمل می کنیم برای هر کدوم از۵به توان۵ شماره ممکن یک حالت از جواب هارو به صورت متمایز در نظر می گیریم؛مثلا من برای عدد 20456
حالت بله بله بله بله خیر خیر خیر بله بله بله بله بله رو در نظر می گیرم و این عدد رو در مجموعه های A6 تا A9 قرار میدم چون جواب بله بوده و در مجوعه های A10 تا A12 قرار نمیدم چون جواب خیر بوده ودر مجموعه های A13تا A17 هم اون رو قرار میدم چون جواب بله بوده و به این ترتیب اگه جواب سوال های من رو به ترتیب بالا بده من متوجه میشم شمارش 20456 بوده و چون تعداد جواب هایی که با ۱۲ تا بله یا خیر میشه بسازیم(۲به توان۱۲)بیشتر از عددهای ممکنه(۵به توان۵)بنابراین برای هر عدد میشه یه حالت متمایز از جواب در نظر گرفت و با توجه به اون جواب ها اعضای مجموعه ها رو تشکیل داد؛یعنی هرجا که خواستیم جواب بله باشه عدد رو در مجموعه مورد نظر قرار میدیم و هرجا که خواستیم خیر باشه عدد رو در مجموعه موردنظر قرار نمیدیم و خب هر جواب هم برای یک عدده و بنابراین با این ۱۷ سوال و از روی جواب های فرد میشه فهمید شمارش چنده

منم کاملا موافقم، بسیار جامع و عالی تحلیل کردید.
برنده امشب معمای پرگاس شما هستید و جواب قبلی تون هم جواب صحیح معما است که فردا در ساعت مقرر نمایش داده میشه، حتما ببینید.
جایزه شما هم الان به کیف پول اضافه شد.
پیروز باشی
 مریم رضائی
مریم رضائی
ممنون
 آیدا حسین زاده
آیدا حسین زاده
سلام برنده بشیم چی بهمون تعلق میگیره؟

سلام
وابسته به نوع معما از 10 تا 40 هزار تومان به موجودی کیف پول تون اضافه میشه.
 نگار پوراحمدی
نگار پوراحمدی
سلام خسته نباشید پاسخ:
۱۷سوال کمترین تعداد پرسشی هست که میشه با جواب بله و خیر انجام داد؛تا مطمئن شد میشه عدد رو با این ۱۷ سوال فهمید؛میدونیم شماره دوستمون ۵ رقمیه؛حالا اگه منظور عدد ۵ رقمی باشه که تعداد حالت های ممکن برای شماره دوستمون میشه 90000حالت و اگه شماره دوستمون به صورت کد باشه میشه 100000 حالت چون اولین رقم از سمت چپ میتونه صفر هم باشه؛در اینجا جواب برای هردو حالت ۱۷ سواله؛دلیلش اینه که ما برای این که مطمئن بشیم عدد رو میفهمیم باید سوالا طوری طراحی بشه که پس از آخرین سوال فقط یک حالت برای عددمون باقی مونده؛و اگر که ما بخوایم برای هر عدد یک حالت از جواب سوال هامون رو هم در نظر بگیریم؛باید تعداد حالت های جواب سوال هامون برابر با تعداد حالت های ممکن جواب باشه؛بنابراین تعداد حالت های جواب های سوال هامون باید حداقل به تعداد حالت های ممکن برای شماره ۵ رقمی باشه؛در این صورت میشه برای هر ۵ رقم یک حالت جواب در نظر گرفت و فهمید اون ۵ رقم چه ارقامی هستند؛خب از اونجا که نوع جواب های ما بله خیر و دو حالتی هستند؛ تعداد حالت های جوابمون براب با ۲ به توان تعداد پرسش هایی هست که میپرسیم؛ وبنابراین
دو به توان n باید بزرگتر مساوی90000باشه(اگه عدد ۵ رقمی باشه)
دو به توان n باید بزرگتر مساوی 100000باشه(اگه کد ۵ رقمی باشه)
و برای هردو حالت کوچک ترین nطبیعی ممکن ۱۷ هست؛بنابراین میشه با ۱۷ سوال فهمید اون پنج رقم کدوم ارقام

سلام
ممنون از نگار عزیز بابت توضیحات کامل شون.
فردا معمای بعدی منتظرتون هستیم به امید برنده شدن.
 فاطمه سلیمانی
فاطمه سلیمانی
۱۷سوال کمترین تعداد پرسشی هست که میشه با جواب بله و خیر انجام داد؛تا مطمئن شد میشه عدد رو با این ۱۷ سوال فهمید؛میدونیم شماره دوستمون ۵ رقمیه؛حالا اگه منظور عدد ۵ رقمی باشه که تعداد حالت های ممکن برای شماره دوستمون میشه 90000حالت و اگه شماره دوستمون به صورت کد باشه میشه 100000 حالت چون اولین رقم از سمت چپ میتونه صفر هم باشه؛در اینجا جواب برای هردو حالت ۱۷ سواله؛دلیلش اینه که ما برای این که مطمئن بشیم عدد رو میفهمیم باید سوالا طوری طراحی بشه که پس از آخرین سوال فقط یک حالت برای عددمون باقی مونده؛و اگر که ما بخوایم برای هر عدد یک حالت از جواب سوال هامون رو هم در نظر بگیریم؛باید تعداد حالت های جواب سوال هامون برابر با تعداد حالت های ممکن جواب باشه؛بنابراین تعداد حالت های جواب های سوال هامون باید حداقل به تعداد حالت های ممکن برای شماره ۵ رقمی باشه؛در این صورت میشه برای هر ۵ رقم یک حالت جواب در نظر گرفت و فهمید اون ۵ رقم چه ارقامی هستند؛خب از اونجا که نوع جواب های ما بله خیر و دو حالتی هستند؛ تعداد حالت های جوابمون براب با ۲ به توان تعداد پرسش هایی هست که میپرسیم؛ وبنابراین
دو به توان n باید بزرگتر مساوی90000باشه(اگه عدد ۵ رقمی باشه)
دو به توان n باید بزرگتر مساوی 100000باشه(اگه کد ۵ رقمی باشه)
و برای هردو حالت کوچک ترین nطبیعی ممکن ۱۷ هست؛بنابراین میشه با ۱۷ سوال فهمید اون پنج رقم کدوم ارقامن

سپاس فاطمه عزیز
بسیار کامل و عالی توضیح دادین.
آفرین به شما
 فاطمه سلیمانی
فاطمه سلیمانی
ببخشید مال من درست بود /

سلام فاطمه عزیز
بله کاملا درست بود
چون جواب معما نمایش داده شده و لیست برنده ها اعلام شده، اسم شما رو اضافه نکردیم.
امیدواریم معمای فردا جز نفرات برتر باشید
 مهدیه نادری
مهدیه نادری
سلام خدمت تمام عزیزان عوامل پرگاس ، خسته نباشید ، روزتون بخیر
۱۷سوال کمترین تعداد پرسشی هست که میشه با جواب بله و خیر انجام داد؛تا مطمئن شد میشه عدد رو با این ۱۷ سوال فهمید؛میدونیم شماره دوستمون ۵ رقمیه؛حالا اگه منظور عدد ۵ رقمی باشه که تعداد حالت های ممکن برای شماره دوستمون میشه 90000حالت و اگه شماره دوستمون به صورت کد باشه میشه 100000 حالت چون اولین رقم از سمت چپ میتونه صفر هم باشه؛در اینجا جواب برای هردو حالت ۱۷ سواله؛دلیلش اینه که ما برای این که مطمئن بشیم عدد رو میفهمیم باید سوالا طوری طراحی بشه که پس از آخرین سوال فقط یک حالت برای عددمون باقی مونده؛و اگر که ما بخوایم برای هر عدد یک حالت از جواب سوال هامون رو هم در نظر بگیریم؛باید تعداد حالت های جواب سوال هامون برابر با تعداد حالت های ممکن جواب باشه؛بنابراین تعداد حالت های جواب های سوال هامون باید حداقل به تعداد حالت های ممکن برای شماره ۵ رقمی باشه؛در این صورت میشه برای هر ۵ رقم یک حالت جواب در نظر گرفت و فهمید اون ۵ رقم چه ارقامی هستند؛خب از اونجا که نوع جواب های ما بله خیر و دو حالتی هستند؛ تعداد حالت های جوابمون براب با ۲ به توان تعداد پرسش هایی هست که میپرسیم؛ وبنابراین
دو به توان n باید بزرگتر مساوی90000باشه(اگه عدد ۵ رقمی باشه)
دو به توان n باید بزرگتر مساوی 100000باشه(اگه کد ۵ رقمی باشه)
و برای هردو حالت کوچک ترین nطبیعی ممکن ۱۷ هست؛بنابراین میشه با ۱۷ سوال فهمید اون پنج رقم کدوم ارقامن
از تمامی زحمات بی دریغ شما عزیزان ، نهایت سپاس و قدردانی را دارم

ممنون از مهربونی شما
خیلی خوب و کامل توضیح دادید
برقرار باشید
 سونیا مهرور
سونیا مهرور
سلام ببخشید من جواب خانم رضایی رو دیدم کامل و خانم پور احمدی انگار از خانم رضایی کپی کرده بود اخه در معما 8 هم از اخرین دیدگاه خانم ضیغمی کپی کرده بود میشه پیگیر یکنین اینطوری حق اونایی که درست نوشتند ضایع میشه :(

سلام سونیا عزیز، بله حتما.