تعداد شرکت کنندگان
تعداد صحیح
تعداد نادرست
میانگین زمان پاسخ دهی
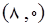و
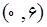مفروض است. یک مستطیل در این مثلث محاط شده به قسمتی که یک رأس منطبق بر مبدأ و دو ضلع آن منطبق بر محورهای مختصات و رأس چهارم مستطیل روی وتر مثلث است. مساحت بزرگ ترین مستطیل ممکن چه قدر است؟پاسخ
12
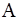روی خطی که دو نقطه ی
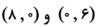را به هم وصل می کند، مساحت مستطیل تغییر می کند. نقطه ی
روی خطی است که از این دو نقطه می گذرد، پس مختصاتش در معادله ی خط صدق می کند.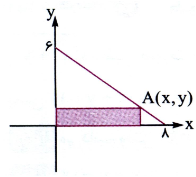
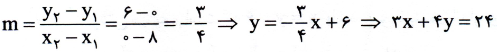
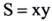است، بنابراین داریم
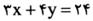و می خواهیم
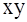ماکسیمم شود:
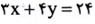ثابت است و می خواهیم
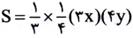ماکسیمم شود پس باید
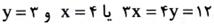باشد، یعنی مساحت ماکسیمم برابر
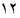است.
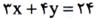پس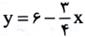
و می خواهیم
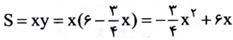ماکسیمم شود، پس مقدار
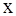باید برابر
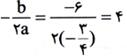باشد و مقدار ماکسیمم مساحت برابر است با
.
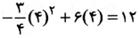