وقتی میخواهیم از میان حروف A , A , A , R , R , M , D , S , L سه حرف انتخاب کنیم، با دو وضعیت کلی مواجه میشویم. یکی این که در 3 حرف انتخابی هیچ حرفی تکرار نشده باشد، یعنی حرف تکراری نداشته باشد و حالت دیگر این که در 3 حرف انتخابی حرف تکراری وجود داشته باشد. (که این خود، شامل چند حالت دیگر هم میشود.) پس تعداد طرق هر یک از این حالت ها را محاسبه میکنیم:
حالت اول: اگر هیچ یک از حروف تکرار نشوند: یعنی از بین حروف A , R , M , D , S , L سه حرف انتخاب شود. پس تعداد حالت های آن برابر است با:
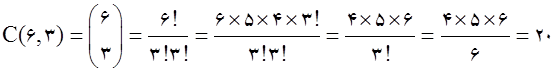
حالت دوم: اگر در میان سه حرف انتخابی، حرف تکراری وجود داشته باشد، حالات زیر میتواند رخ دهد:
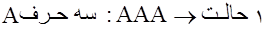
5 حالت
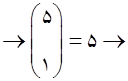
حرف سوم میتواند یکی از حروف R , M , D , S , L باشد.
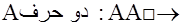
5 حالت
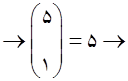
حرف سوم میتواند یکی از حروف A , M , D , S , L باشد.
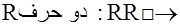
پس تعداد حالاتی که حرف تکراری در سه حرف انتخابی وجود داشته باشد، برابر با
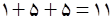
است.
در نتیجه تعداد کل حالات برابر
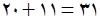
است.
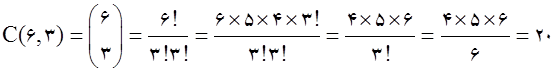
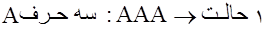
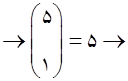 حرف سوم میتواند یکی از حروف R , M , D , S , L باشد.
حرف سوم میتواند یکی از حروف R , M , D , S , L باشد.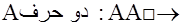
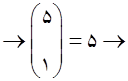 حرف سوم میتواند یکی از حروف A , M , D , S , L باشد.
حرف سوم میتواند یکی از حروف A , M , D , S , L باشد. 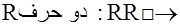
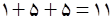 است.
است.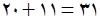 است.
است. 



